介绍
二叉树,是一种树形的数据结构,每个节点最多有两棵子树,有左右之分。
如下图:
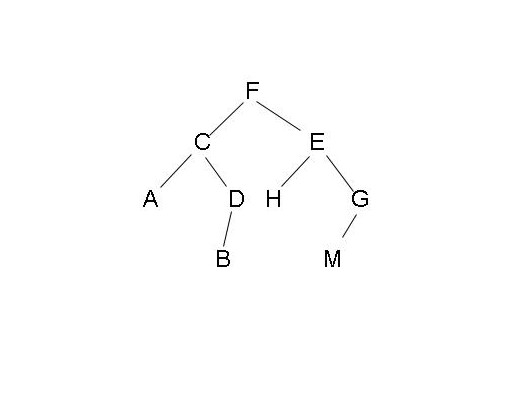
- 头结点:F就是头节点
- 子树:从某一个头结点出发,下面所有的节点都需要算上。如C、E就是F的子树,A、D就是C的子树,B就是D子树。但是D和B并不是C的子数,因为漏掉了A。
- 左子树:就是我左边的所有子树,比如F,就是C/A/D/B全部是F的左子树。C的左子树就是A。
- 右子树:就是我右边的所有子树,比如F,就是E/H/G/M全部是F的右子树,G的右子树就是空,E的右子树就是G。
遍历,有几种方式。
先序(头左右)
任何子树的处理顺序,都是先从头节点,再左子树,然后再右子树。
所以顺序就是 F->C->A->D->B->E->H->G->M中序(左头右)
任何子树的处理顺序,都是先从左节点开始,再到头,最后到右子树。
所以顺序就是 A->C->D->B->F->H->E->G->M后序(左右头)
任何子树的处理顺序,都是先从左节点开始,再到右,最后到头节点。
所以顺序就是 A->D->C->B->E->H->G->M->F
代码
首先创建二叉树
type Node struct {
value string
left *Node
right *Node
}
func createNode() *Node {
//F的全部左子树
nodeB := &Node{
value: "B",
left: nil,
right: nil,
}
nodeD := &Node{
value: "D",
left: nodeB,
right: nil,
}
nodeA := &Node{
value: "A",
left: nil,
right: nil,
}
nodeC := &Node{
value: "C",
left: nodeA,
right: nodeD,
}
// F的全部右子树
nodeM := &Node{
value: "M",
left: nil,
right: nil,
}
nodeG := &Node{
value: "G",
left: nodeM,
right: nil,
}
nodeH := &Node{
value: "H",
left: nil,
right: nil,
}
nodeE := &Node{
value: "E",
left: nodeH,
right: nodeG,
}
nodeF := &Node{
value: "F",
left: nodeC,
right: nodeE,
}
return nodeF
}
基础的遍历
递归遍历
func main() {
node := createNode()
//pre(node)
middle(node)
//after(node)
}
// 先序
func pre(root *Node) {
if root == nil {
return
}
fmt.Println(root.value)
pre(root.left)
pre(root.right)
}
// 中序
func middle(root *Node) {
if root == nil {
return
}
middle(root.left)
fmt.Println(root.value)
middle(root.right)
}
// 后续
func after(root *Node) {
if root == nil {
return
}
after(root.left)
after(root.right)
fmt.Println(root.value)
}
有趣的现象
比如一下二叉树:
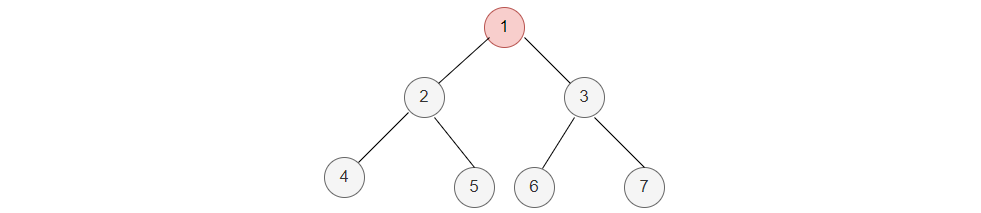
我们比如说是按照先序的打印,就是头左右的来看,每个节点都会出现三次的打印以及调用。
如:先来到1节点,左边有,就来到了2节点,接着来到了4节点,然后4节点的左节点为nil,返回4,接着去4的右节点,为nil又返回4。
然后返回到2节点,接着去5节点,5节点左为空,返回5,来到5的右节点,为空返回5。
....以此类推,每个节点都会出现三次。最终走过的路线就是:1,2,4,4,4,2,5,5,5,2,1,3,6,6,6,3,7,7,7,3,1 每个节点都会到达3次。
这不能说明什么,重要的是下面才有趣呢。
先序遍历:就是每次第一次到达节点的时候,就打印,如:1,2,4,5,3,6,7
中序遍历,就是每次第二次到达节点的时候,就打印,如:4,2,5,1,6,3,7
后续遍历,就是每次第三次到达节点的时候,就打印,如:4,5,2,6,7,3,1
这说明什么,说明每个节点都有机会去左、右、头节点三个去转一圈。所以这就是 递归序 也是在二叉树上面做动态规划的基础。
ok,先到这。
压栈遍历
前序
有这么几个顺序:先把头节点压入栈,然后再pop,pop就打印,如果当前栈顶又右节点,压入栈,如果有左节点,压入栈,也就是先压右,再压左。
func stackPre(head *Node) {
var stack []*Node
stack = append(stack, head)
for len(stack) != 0 {
top := stack[len(stack)-1]
fmt.Println(top.value)
//pop
stack = stack[:len(stack)-1]
if top.right != nil {
stack = append(stack, top.right)
}
if top.left != nil {
stack = append(stack, top.left)
}
}
}
后序
一样,也是有顺序的,先把头压入栈,然后再pop的时候,但是不打印,而是重新放入一个新的栈。但是顺序反了,如果有左,压入左,如果有右,压入右。
然后需要重新打出来栈来。
func stackAfter(head *Node) {
var stack []*Node
var bakStack []*Node
stack = append(stack, head)
for len(stack) != 0 {
top := stack[len(stack)-1]
bakStack = append(bakStack, top)
//pop
stack = stack[:len(stack)-1]
if top.left != nil {
stack = append(stack, top.left)
}
if top.right != nil {
stack = append(stack, top.right)
}
}
for i := len(bakStack) - 1; i >= 0; i-- {
fmt.Println(bakStack[i].value)
}
}
中序
这个稍微麻烦点,有两个分支:
- 整条左边界依次入栈
- 如果左边界为nil,弹出加打印,然后右数入栈。
func stackMiddle(head *Node) {
if head == nil {
return
}
var stack []*Node
for len(stack) != 0 || head != nil {
if head != nil {
stack = append(stack, head)
head = head.left
} else {
head = stack[len(stack)-1]
fmt.Println(head.value)
// pop
stack = stack[:len(stack)-1]
head = head.right
}
}
}
按层遍历
实现从上到下,从左至右的遍历,如最上图,遍历结果为: F->C->E->A->D->H->G->B->M
我们可以通过队列的方式来:
- 先把头结点加入到队列里面去
- 条件为,如果队列不为空则结束
- 先把队列的头poll出去,然后打印,也就是弹出就打印。
- 然后左节点不为空,加进去队列中,右节点不为空,也加进去队列中。
func level(node *Node) {
var levelArr []*Node
levelArr = append(levelArr, node)
for len(levelArr) != 0 {
current := levelArr[0]
fmt.Println(current.value)
levelArr = levelArr[1:]
if current.left != nil {
levelArr = append(levelArr, current.left)
}
if current.right != nil {
levelArr = append(levelArr, current.right)
}
}
}



