前缀和，相当于把数组进行预处理，把一个数组的某项下标之前(包含当前元素)的所有数组的元素的和，先计算出来生成新的数组，后续要用到该数组的位置和，则无需再次遍历原数组即可快速获取结果，时间复杂度为O(1)。

前缀和

具体解释

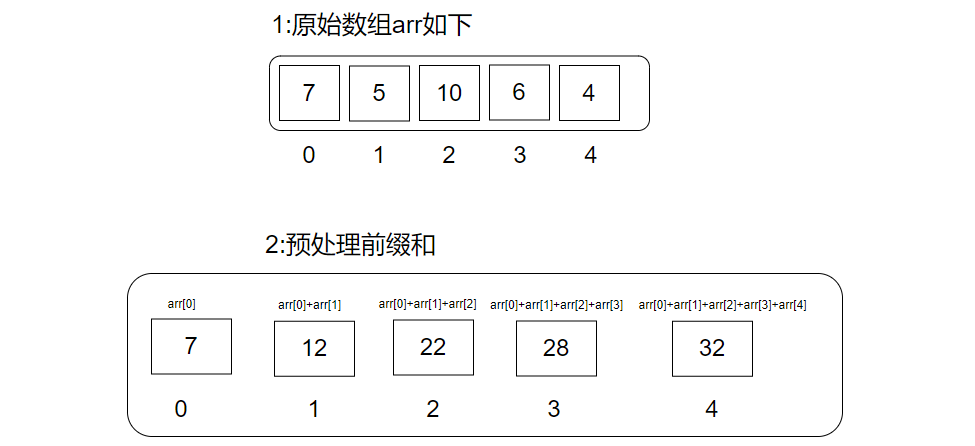
原数组arr[7,5,10,6,4]和预处理前缀和后的数组pre[7,12,22,28,32]之间的关系，如同:
pre[0]=arr[0]
pre[1]=arr[0] +arr[1]
pre[2]=arr[0] +arr[1] +arr[2]
pre[3]=arr[0] +arr[1] +arr[2] +arr[3]
pre[4]=arr[0] +arr[1] +arr[2] +arr[3] +arr[4]
这种也叫差分，称为数组arr叫数组pre的差分数组。

前缀和作用

没有前缀和数组，则每次需要计算arr数组中元素和，arr[1]+arr[4],都需要遍历一次数组，时间复杂度为 O(n)
有了前缀和数组，只是预处理的时候时间复杂度为O(n),后续都是O(1)，大大提高了效率

算法解释

如获取arr[1]+arr[4],可以类比为 arr[0]+arr[1]+arr[2]+arr[3]+arr[4]-arr[0] = 25
那
arr[0]+arr[1]+arr[2]+arr[3]+arr[4] = pre[4]
arr[0]=pre[0]
就如同是 pre[4]-pre[0] = 25

代码

//   []int{7, 5, 10, 6, 4}  l=1,r=4
func SumPre(arr []int, l, r int) {
    preSum := preSumArray(arr)
    sum := getSum(preSum, l, r)
    fmt.Println(sum) // 25

}

func preSumArray(arr []int) []int {
    var preArr []int
    sum := 0
    for _, val := range arr {
        sum += val
        preArr = append(preArr, sum)
    }
    return preArr
}

func getSum(sum []int, l, r int) int {
    if l < 0 || r > len(sum) {
        // 讲道理，这里应该报错的
        return 0
    }
    if l == 0 {
        return sum[r]
    }
    return sum[r] - sum[l-1]
}

详细例子：累加和为k的最长连续子数组位数

如：数组[20,12,24,3,18]如果k为64，则20+12+24=64,最长子数组就是[20,12,24]，也就是3 如果k为39，那最长子数组就是12+24+3,也就是最长子数组为[12,24,3]，也就是3

思路一，暴力破解

使用三个for循环，动态的去计算 时间复杂度为o(N^3)，我不讨论

思路二，使用前缀和

代码

func MationSum(arr []int, k int) {
    preMap := map[int]int{0: -1} //需要初始化值，不然如果在开始位或者全位的时候，sum-k=0，map中找不到
    sum := 0
    longest := -1
    for index, item := range arr {
        sum += item
        temp := sum - k
        j, ok := preMap[temp]
        if ok && index-j > longest {
            longest = index - j
        }
        if _, ok := preMap[sum]; !ok { //如果不存在则加进去，如果没有这个判断，相当于查询最后的最长子数组了
            preMap[sum] = index
        }
    }
    fmt.Println(longest)
}

时间复杂度为O(N)