二分法查找是建立在有序的集合中，是搜索算法中入门级别的，下面我们逐步分解。

释义

我们通过循环来查找，循环退出的条件为：
1：下标m的值跟查找的数相等。
2：左游标>右游标

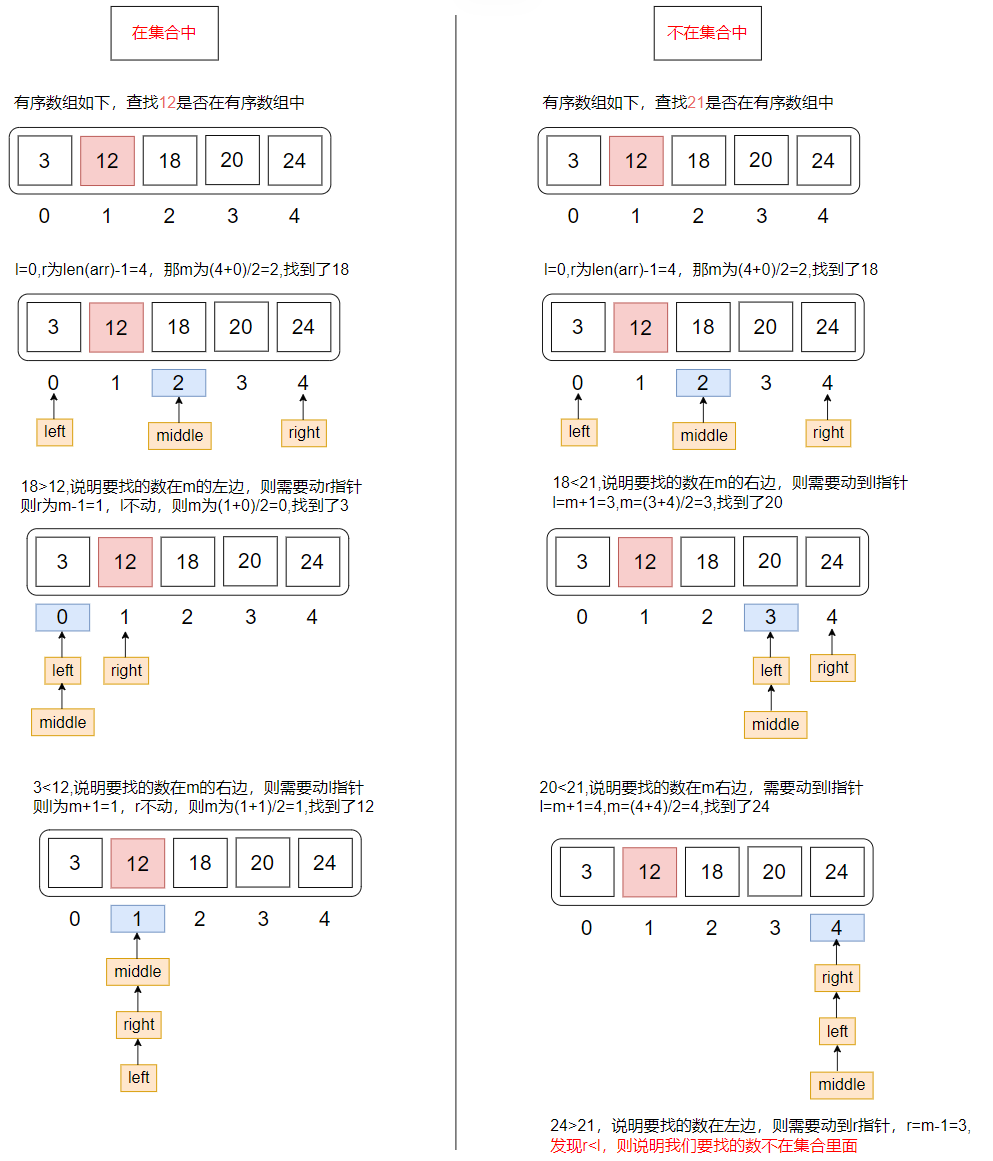
代码

func SearchBinary(arr []int, num int) bool {
    if len(arr) == 1 {
        return arr[0] == num
    }
    left := 0             // 左游标
    right := len(arr) - 1 // 右游标

    for right >= left {
        // middle := (left + right) / 2 // 这种写法有丢丢隐患，比如l=15亿，r=15亿，则他们的和就溢出了
        //middle := left + (right-left)/2  // 这样就绝对不会溢出
        middle := left + (right-left)>>1 // 位移 >>是/2的另一种表达
        if arr[middle] == num {
            return true
        }
        if arr[middle] > num {
            //说明num在m的左边，则left不动
            right = middle - 1
        } else if arr[middle] < num {
            // 说明num在m的游标，则right不动
            left = middle + 1
        }
    }
    return false
}

比较

我们拿一个循环查找来看

func CircleSearch(arr []int, num int) bool {
    defer DeferTime("circleSearch")()
    for _, item := range arr {
        if item == num {
            return true
        }
    }
    return false
}

func DeferTime(funcName string) func() {
    startTime := time.Now()
    return func() {
        sub := time.Now().Sub(startTime).Milliseconds()
        fmt.Printf("%s exec time millise : %d \n", funcName, sub)
    }
}

同样的在一个如1亿中查找一个数是否在靠后的位置(最坏的时间复杂度)

    for i := 0; i < 10000000; i++ {
        arr = append(arr, i)
    }
    binary.SearchBinary(arr, 8888888) //二分法查找
    binary.CircleSearch(arr, 8888888) //循环查找

输出

binarySearch exec time millise : 0 
circleSearch exec time millise : 30